Singular Value decomposition

$A = U Σ V^{⊤}, U \in R^{m \times m}, V \in R^{n \times n}$

$U$ : orthonormal colums, orthonormal basis of $C o l A$

$V$ orthonormal rows, orthonormal basis of $R o w A$

$Σ$ : diagnal matrix with decreasing order

unique orthonormal basis이지는 않는다. Gram-schmidt를 적용할 때, $V$ 를 무엇으로 잡는냐에 따라 달라지듯이, 그 basis는 다양하게 나타날 수 있다.

Reduced Form of SVD

A = U Σ V^{⊤} = i = 1 \sum n σ_{i} u_{i} v_{i}^{⊤}

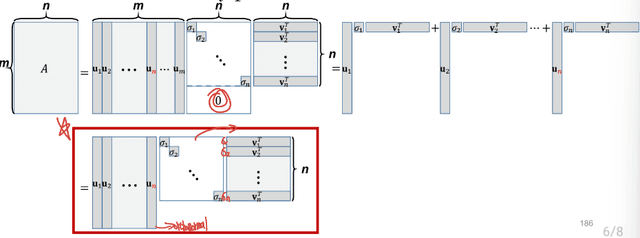
See as Eigen decomposition

$A V = U Σ$
: $V^{- 1} = V^{⊤}$ : $V$ 는 orthonormal columns를 가지므로, 해당 식이 성립한다.

$A A^{⊤} = U Σ V^{⊤} V Σ^{⊤} U^{⊤} = U Σ Σ^{⊤} U^{⊤} = U Σ^{2} U^{⊤}$
$A^{⊤} A = V Σ^{⊤} U^{⊤} U Σ V^{⊤} = U Σ^{⊤} Σ V^{⊤} = V Σ^{2} V^{⊤}$ : $V^{⊤} V = I_{n}$ : $V$ 가 orthonormal 하므로, $i = i$ 에 대해서는 1, $j \neq = i$ 에 대해서는 0이 된다. 일종의 Eigen decomposition을 사용하게 되는 것으로 볼 수 있다.

Orthogornal eigenvector matrices $U$ and $V$ : condition of Diagonalization
Eigenvaleus in $Σ^{2}$ that are positive: symmetric matrix라면 always Eigendecomposition이 존재한다. 그리고 이는, SVD와 동일하다.
Eigenvalues in $Σ^{2}$ that are shared by $A A^{⊤}$ and $A^{⊤} A$ : $A A^{⊤}$ and $A^{⊤} A$ are symmetric positive (semi-) definite.

Spectral Theorem of Symmetric Matrices: $A A^{T}$

for square matrix A, $(A A^{⊤})^{⊤} = A A^{⊤}$ : symmetric.

symmetric matrix: is always orthogonally diagonalizable: 항상 SVD 가능하다.

eigenspaces are mutually orthogonal, eigenvectors corresponding to different eigenvalues are orthononal: 각기 다른 eigenvalue를 가지게 된다.

Positive Definite Matrices

positive definite: $x^{⊤} A x > 0, \forall x \neq = 0$

positive semi-definite: $x^{⊤} A x \geq 0, \forall x \neq = 0$

$x^{⊤} A A^{⊤} x = ∣∣ A^{⊤} x ∣ ∣^{2} \geq 0$ 이므로, positive-semi-definite하다. 따라서, Eigenvaluees in $Σ^{2}$ 는 모두 positive하다.

Low Rank Approximation

SVD can be represented as sum of outer products:

A = U Σ V^{⊤} = i = 1 \sum n σ_{i} u_{i} v_{i^{⊤}}

Approximation of $A$ : $\hat{A_{r}}$ : $ar g min_{A_{r}} ∣∣ A - A_{r} ∣ ∣_{F}$ : (Frobeneius norm: error값을 제곱해서, 모든 element를 더한 후, 루트를 씌운것이 된다.)
$r ank (A_{r}) \leq r$ 가 된다.

Optimal solution: $\hat{A_{r}} = i = 1 \sum r σ_{i} u_{i} v_{i^{⊤}}$ , 작은 $σ$ 는 무시하게 된다.

Dimension-Reducing transformation

Linear Transformation: $X \in R^{m \times n}$ , $Y = G^{⊤} X$
m차원을, n차원으로 축소시키는 $G$ 를 찾는다.

$G$ 는 orthonormal하며, similarity between data items: $S = X^{⊤} X$ 를 가장 잘 보존시키는 행렬이 되어야 한다.
Y의 similarity는, $Y^{⊤} Y = (G^{⊤} X)^{⊤} G^{⊤} X = X^{⊤} G G^{⊤} X$ 와 같이 쓰인다.
Then,

\hat{G} = ar g G min ∣∣ S - X^{⊤} G G^{⊤} X ∣ ∣_{F}

optimal solution: $\hat{G} = U_{r} = [u_{1} u_{2} \dots u_{r}]$ . when, $X = U Σ V^{⊤}$